隐私作为公共产品
在Namada上，隐蔽集是受到补贴的，以便初始用户不依赖于存在足够大的隐蔽集。相反，补贴被编程以确保无论隐蔽集的大小如何，都有足够的激励使资产进入隐蔽集。
隐私应该得到补贴，以下是原因
背景 在当代经济学中，如果一种商品是不竞争且不排斥的，那么它被归类为公共物品。简而言之，如果一个人的消费不会妨碍其他人的消费，那么该商品就是不竞争的。如果一个商品存在时，任何人都无法阻止其被消费，那么它就是不可排斥的。
公共物品的例子包括灯塔、交通信号灯、正常运作的司法系统、开放源代码技术、公共思想、卫生设施等等。
严格来说，隐私本身并不是公共物品，因为虽然它不是竞争性的，但它是可以被排除的。阻止用户进入受保护的隐私领域是很容易的（理论上，Namada当然是无需许可的）。然而，隐私仍表现出与公共物品相关的特性，即具有积极外部性。当一个人的隐私使用对另一个人有益时，就产生了这种积极外部性，而这种积极外部性是不可排除的。更具体地说，当一个用户进入受保护的隐私领域时，它增加了已经在该领域内的所有人的总体隐私，而不能排除任何已经在该领域内的人受益。
隐私的正外部性
正外部性可以通过一个玩具示例（以及相应的图表）来解释。
为了简化起见，假设经济中的每个“代理人”在他们的偏好方面都是相同的。我们假设用户重视存在于一个隐私集中的机会，并且随着隐私集的大小增加，隐私集的价值也增加。显然，一个0人的隐私集是没有价值的。此外，我们假设隐私集的大小每增加一个人都具有“递减的边际效益”属性，即每增加一个用户对整体隐私的贡献都减少。随着隐私集不断增大，有人进入隐私集的额外好处变得微不足道。在经济学中，我们倾向于通过一个“效用”函数来表示这一点，这个函数存在的目的是为了衡量代理人的成本和价值。一个展示上述特性的效用函数的自然选择如下：
其中， n 是隐私集的大小。尽管这是离散的，为了简单起见，我们将在连续域中进行工作。
此外，我们假设存在一些不可避免的“成本” c，用户进入隐私集需要承担这些成本。在现实世界中，这可能对应于学习零知识密码学、处理私钥和用户在这个过程中可能承担的其他形式的“努力”和风险。正如Gavin Birch指出的，还有未能将资产借出或在透明系统中质押资产所带来的机会成本。希望有一天我们也能找到方法在一个隐蔽集中实现这一点。
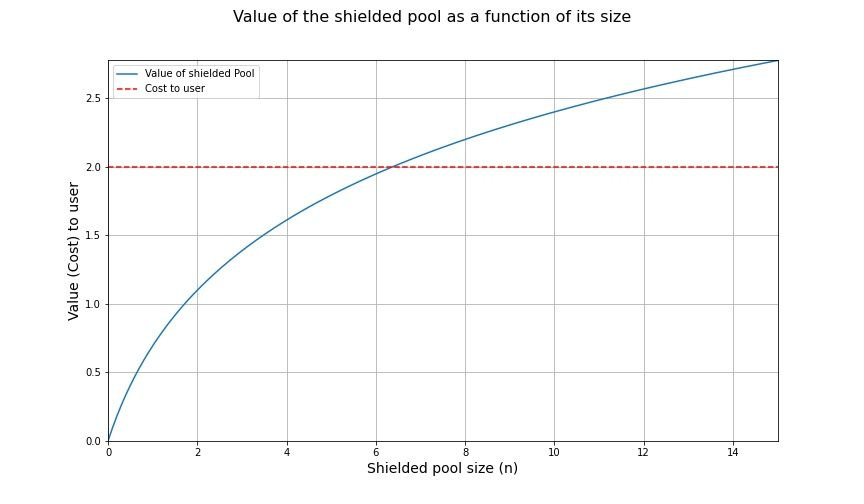
隐蔽池成本与效益权衡的可视化
社会成本
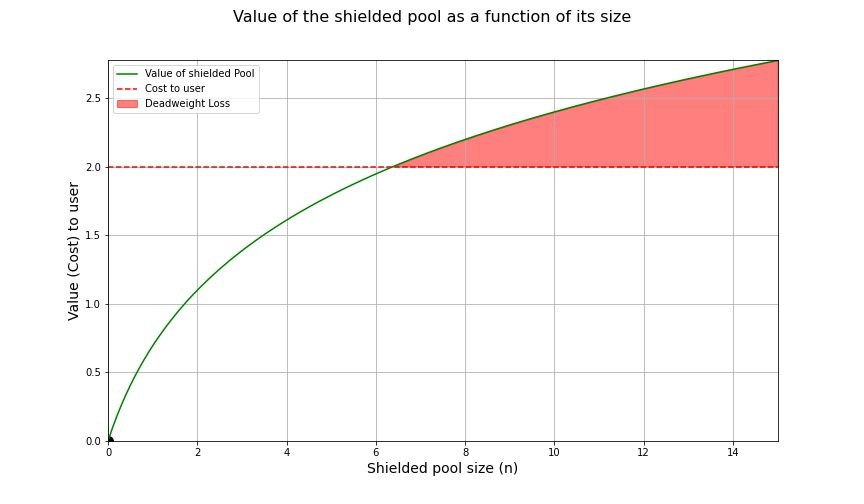
由于与进入隐私集相关的正外部性，如果用户无法协调，那么在经济中将会失去一些未实现的价值。当没有其他用户在隐私集中时，隐私集的价值为零。在现代经济学中，这种在整个经济中所有用户之间累积的失去价值被称为死权损失。下面通过阴影区域显示了死权损失，它位于价值和个体进入的成本之间。
隐蔽池不存在的死权损失的可视化
因此，如果协议可以激励足够多拥有大规模资产的用户加入隐私集，以确保在隐私集中留下足够的价值，协调问题就会得到解决。如果“社会规划者”完全了解需要多少用户才能达到这个“临界点”价值n∗，她可以提供恰好足够的补贴来激励前n∗用户使用协议，而不多给。
纠正外部性
我们提出了一种替代方法，我们可以声称：
如果补贴s(n)与隐蔽池的大小成反比，即s(n)∝n^(-1)，那么对于足够大的比例常数k，补贴将激励正确数量的用户加入系统。此外，这种激励方案具有有限和可预测的额外好处。这不是唯一可能的解决方案，但是是其中之一，看起来是自然的选择。
示例1：补贴不足
上述补贴虽然稍微降低了门槛，但不足以激励用户加入网络。在上面的示例中，隐私集的大小将从 0 增加到 ~0.6。为了达到临界质量，我们需要激励至少达到一定规模的隐私集n≈5.4
示例2：充足的补贴
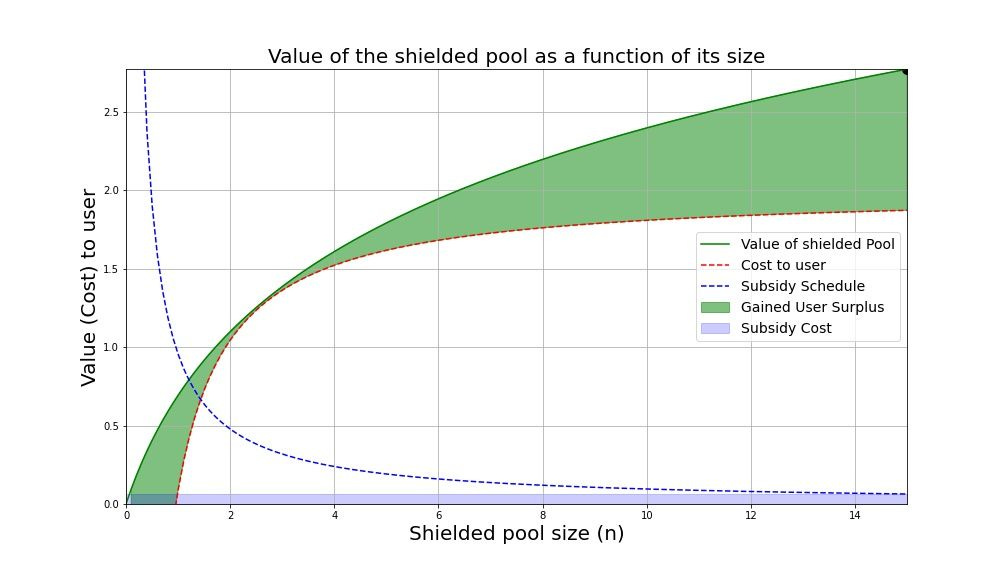
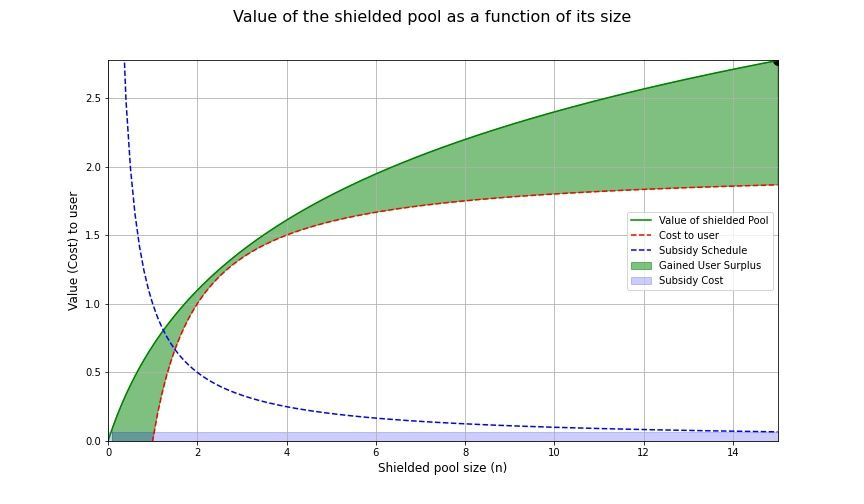
如果我们将激励措施提高到与用户的成本完全成正比，那就足够了。以这种方式设计补贴的另一个好处是补贴变得易于解释；补贴总额正是任何单个用户的成本，分配给所有用户。
补贴时的视觉效果当k=c
现在，最小化曲线之间面积的点由用户成本（考虑补贴后）与屏蔽池的价值相切的点给出。挑战：推导这个！
提示：考虑最小化面积和积分的导数是曲线本身......
示例3：最优补贴
这导致我们：
们还需要确保两条曲线恰好有一个交点
这两个联立方程可以解为k∗
最优的k∗进行数值求解并如下所示
这最大限度地减少了补贴成本，但代价是失去了一些简洁的解释:)
结论
本文的关键要点是，进入屏蔽组具有正外部性。如果没有补贴，就会存在递归协调问题。用户希望输入足够大的屏蔽装置。然而，屏蔽集无法实现，因为它的存在首先依赖于进入屏蔽集的资产。
有了补贴，初始用户就不再依赖于足够大的屏蔽装置的存在。相反，补贴的目的是确保无论屏蔽集的规模有多大，都有足够的激励资产进入屏蔽集。
此外，在合理的假设下，精心构建的补贴具有几个良好的特性。其总成本是有限的，与屏蔽装置的大小无关，并且完全可预测。此外，它提供了无限的社会价值（仅受限于世界上所有资产的总规模）。最后，解决方案k=c很容易实现，中学生也能理解该方程。
如需反馈和意见，请访问Namada 论坛上的相关主题。
我要感谢 Gavin Birch 和 stellarmagnet 迄今为止富有洞察力的评论：D
原文发布时间为2023 年 1 月 17 日