理解 MASP/CC

MASP与CC实施了多资产功能和可编程资产转换。本文解释了密码学的工作原理以及使用这些电路可以构建哪些其他私人应用程序。

Convert电路 (CC) 可以以保护隐私的方式分发奖励

Multi Asset Shielded Pool和Convert Circuit (MASP)

背景

在本文中，我将尝试在高层次上解释MASP，然后在稍微更加技术性的低层次部分提供更详细的解释（但仍然不足以完全理解它）。然后我将思考该技术的可能应用，这些应用超出了Namada上展示的内容。这是一篇较长的文章，可能需要分成两次阅读。我建议将阅读分成多个部分，因为文章涉及内容较多。任何反馈都受欢迎。

用5岁孩子能理解的方式解释

在非常高的层次上：[1]

存在两组不同的资产：

1. 隐私集合

2. 透明集合

从用户的角度来看，隐私集合中的所有交易在外表上都难以区分。更具体地说，用户可以看到笔记被创建以及无效化器（使笔记无法花费的对象）。

**透明集合：**从用户的角度来看，透明集合中持有的所有代币等同于在任何其他透明生态系统中持有代币。用户可以进行资产从一个地址转移到另一个地址，还可以通过Namada上部署的桥接设施进行跨链资产操作。

隐私集合

隐私资产的隐蔽： 资产被铸造到隐私集合中，需要通过有效的零知识证明产生一个“笔记”。零知识证明旨在证明以下几点：

1. 笔记将以哪种资产类型命名[2]

2. 资产的数量

3. 拥有笔记的地址

4. 基础资产被发送到托管账户

**资产转移：**隐私到隐私的资产转移是通过零知识证明构建的。这些证明确保：

1. 被花费的笔记尚未被花费

2. 被花费的笔记以前曾被创建

3. 花费笔记的用户确实拥有它们

4. 交易本身保持平衡（没有创建或销毁资产）

**隐私资产的解锁：**用户在公开地透露了用于铸造过程的信息以及其无效器后，就能够获取等值资产的所有权，这些资产由原生有效谓词（Validity Predicate）释放出来。原生VP确保证明是有效的，且资产已转换为其最新时代[3]。

转换电路（CC）

在Namada中有两个电路。MASP电路处理隐私资产（笔记）的铸造和销毁。**转换电路（CC）**是一个独立的电路，与MASP电路协同工作，允许根据预定义的公共转换表在隐私池中的资产之间进行转换。

在高层次上，转换电路使资产能够在不泄露隐私或揭示任何元数据的情况下进行转换。请注意，这些转换在字面上是真正的转换，通过铸造和销毁机制实现，这意味着根本不需要流动性池或交易对手，因为转换就是转换，而不是交换。这是一个重要的特点，因为它对于理解任何统一的隐私池至关重要。

在Namada中，转换电路的存在是为了奖励维护在隐私池中的隐私资产。这些奖励充当纠正正外部性的原因的补贴。更详细地讨论了如何纠正正外部性，无论是书面的还是视频的方式。

实现这个理念的思路如下：

1. 每种资产都附属于一个时代

2. 资产可以在不同时代之间转换

3. 转换因子为1：（1 + 额外补贴NAM代币）

举个例子：

• 爱丽丝在时代1内将100 NAM的资产进行了隐私操作

• 爱丽丝知道公开可用的CC转换表，该表表示每时代持有的100 NAM将获得1 NAM的奖励

• 在时代2，爱丽丝通过转换电路进行了隐私转移，她获得了时代2内的100 NAM和额外的1 NAM，总共是101 NAM

上述的转换表用于计算Namada的资产持有者的奖励，以鼓励他们在隐私集合中持有资产。

在较低层次

了解如何进行隐私转移的方式，重要的是了解在Namada中如何构建零知识SNARKs（简洁非交互式知识论证）。这是因为每个隐私转移的有效性基本上是由其自己的零知识论证证明的。

首先，每个zk-SNARK需要“公共参数”，这些参数是从“受信任的函数”生成的。 这个受信任的函数接受安全参数 λ 作为输入，并产生公共参数 pp 和毒害废物 τ 作为输出。

• 有一个证明算法，它接受隐私转移的私人详细信息，并输出一个证明 π，证明了该转移是有效的

• 有一个验证算法，它接受隐私转移的公共详细信息和一个证明 π，只有在证明算法从相应转移的私人详细信息生成 π（在密码学假设下）时才输出1

• 有一个模拟器算法，它在输入 pp、λ 和“假”隐私转移的公共详细信息时，可以生成一个“假”证明 π，而不知道相应的私人详细信息。

受信任 是指当函数 f trusted (λ) 被评估时，只有公共参数 pp λ 被保留，而毒害废物 τ 被销毁且无法恢复。

τ 的存在 用于证明证明 π 具有零知识性，验证算法除了验证其有效性外，从 π 中学不到任何新信息。

注释承诺： 注释承诺是通过同态Pedersen承诺定义的。同态Pedersen承诺是通过两个生成器创建的：值基和随机性基。

为了涵盖多个资产，Namada使用一个动态生成器为每个资产派生一个新的值基。此外，该动态生成器使用伪随机性来确保资产类型之间的关系是计算上不可行的。

从论文中得知：

• 资产生成器（也称为值基）是Jubjub曲线上的有效ctEdwards曲线点，其压缩位表示是资产标识的BLAKE2s图像

• 资产生成器的BLAKE2s预图像定义了资产标识符。

在Sapling中，为了避免攻击者错误地打开价值承诺（从而花费他们不“拥有”的笔记）的能力，必须做出一个安全性假设，即基点（资产生成器）和随机性参数之间不能存在离散对数关系。添加多个资产类型对电路设置提出了额外的假设，即各资产的生成器基点之间也不能存在离散对数关系。这将允许用户错误地跨资产打开价值承诺。

更技术性的、但仍然重要的假设是，不应存在两个可以互相抵消的资产生成器，就像它们是 P 和 [-1]P 一样。通过采取适当的预防措施，可以避免这种情况。

转换电路： 在更低层次，转换电路通过一个转换表和具有多元结构的合成资产来工作。

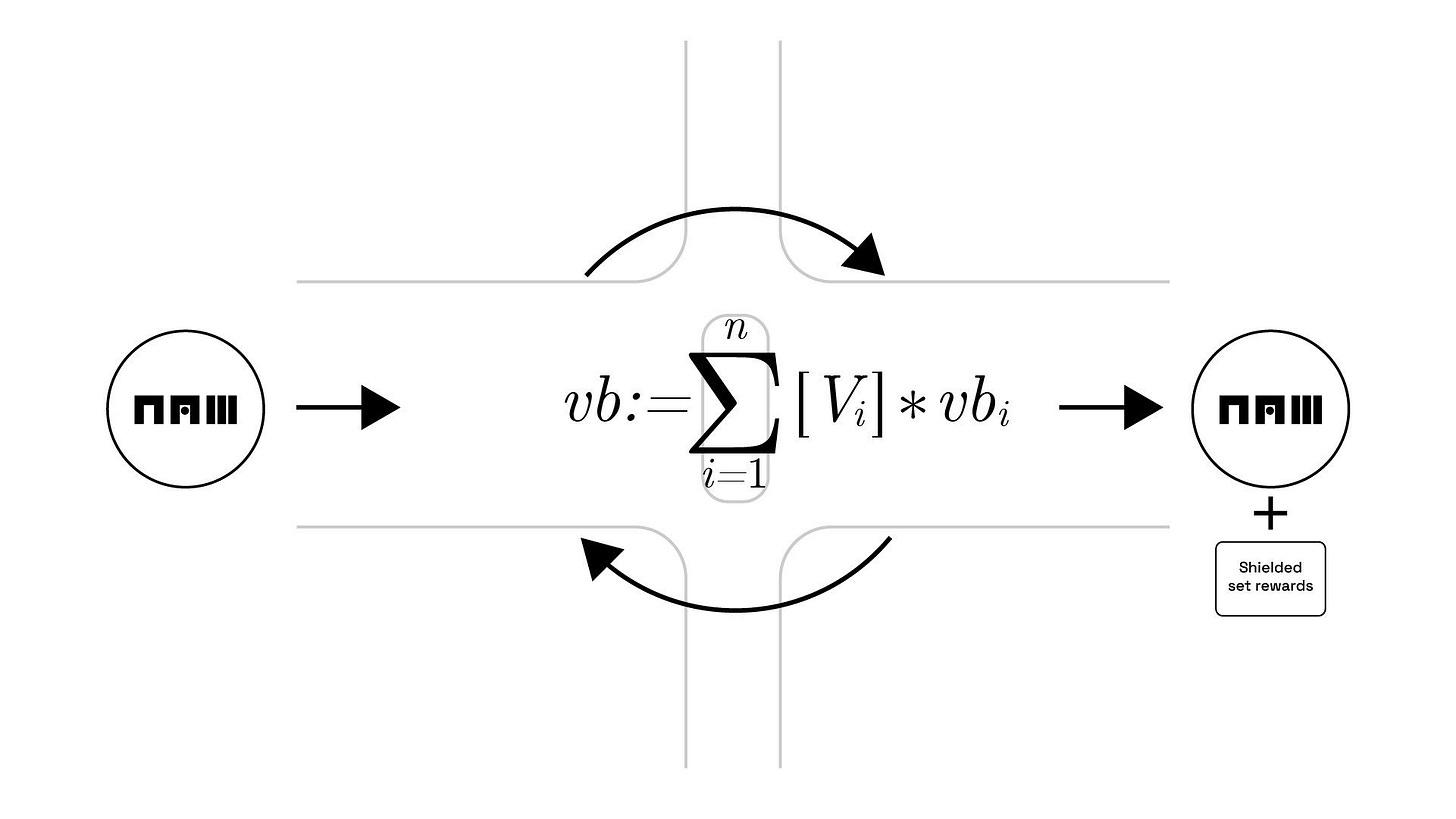
更具体地说，一个有效的预定义转换是一个包含 [(A1, V1), (A2, V2), ...(Ai, Vi), ...(An, Vn)] 的元组（Ai, Vi）的列表，定义了一个新的资产生成器 vbcc，由以下方式给定：

vbcc := Σi=1 ∑n [Vi] * vbi

其中 vbii 是相应的资产生成器 Aii。这可能一开始看起来令人困惑，但如果我们以最简单的形式来考虑，我们可以将转换定义为可以将先前时代的1个NAM代币转换为当前时代的NAM代币的电路，还会获得额外的NAM代币作为奖励。这存在是为了鼓励用户将他们的资产保留在隐私集合中，以资助隐私集合。

应用

这种技术在提供通货膨胀性补贴以外的领域有许多不同的应用。以下是我对潜在创意的一些建议。

隐私税收

假设我们处于一个世界，其中区块链已经成为主流，政府最终能够监控和实施透明方面的税收计划。这在现在并不难实现，因为所有数据都是公开的。人们不再需要提交税务申报，因为税款应该只需自动计算。然而，与此同时，政府正在监控每一笔交易。因此，人们可能希望寻找更加具有隐私性的解决方案（这是正当的）。

通过自定义的CC（转换电路），政府可以在隐私集合内实施财富/收入税。这个转换表可能如下所示：

税率：tax

[−1] NAM 时期 i [+(1−tax)] NAM 时期 (i+1)

对于所需的所得税，需要更深入的思考和研究，但仍然是可能的。

政府将如何在隐私集合中执行此类交易？ 政府可以通过确保所有取消隐私操作都需要使用每个资产的最新指定时期来实施此操作。

因此，税收是在不影响任何隐私保障的情况下实现的。为了“征收”这些税款，政府只需允许铸造等值的资产，这些资产迄今已经通过上述转换电路进行了销毁。

除了作为政府的资金机制用途，这种类型的转换电路还可以用作激励机制（背离而不是奖励）以鼓励隐私交易。例如，对于那些被指定在某个日期之前的时期内的资产，当进行转换时可以征税，以鼓励更频繁的转换。

众筹和投票

与借贷和借款机制类似，转换电路可以用于铸造与“承诺”相关的资产，并且可以完全保护隐私。例如，如果用户与处理提案投票的合同/VP（验证谓词）进行交互，可以允许1个“投票代币”转换为1个“已投票代币”。然后，在投票期结束后，关闭该转换并允许进行反向转换（或更复杂的操作）。这也可以用于众筹，如果在截止日期之前未达到资金筹集目标，可以开启反向转换，否则不开启。

转换电路： 在投票/筹款期间 在投票/筹款截止日期后

隐私预测市场

这显然需要某种值得信赖的预言机，但思想是可以使用转换来创建具有隐私的不受信任的预测市场。以超级碗LVII为例，这在撰写时是相关的。假设我们想要创建一个关于费城老鹰队是否会在今年赢得超级碗的预测市场。这将是一个二元结果，预测市场将如何构建，使得“是”代币在费城老鹰队确实赢得超级碗时可以转换为100 NAM，否则“否”代币可以在他们不赢得时转换为100 NAM。

一个自定义的有效性谓词将处理将新的转换添加到转换表中，并根据预言机价格来关闭/开启它们。

转换电路中的新转换将允许用户存入100 NAM代币，其中包括“是”和“否”代币。用户可以在市场上交易这些代币，而且可以做到保护隐私。这需要用户找到交易对手，可以轻松地在链外找到不同意见的交易对手。至于链上交易对手发现，这可以被整合到协议中（在未来的Anoma区块链上），或通过与成熟的允许交换的市场（例如Osmosis）进行集成，或者通过允许用户在交易一些隐私和不那么信任的前提下进行交易的最小信任前端。

这在具体操作上会是怎样的呢？ 例如，如果我认为费城老鹰队赢得超级碗的概率正好是x，那么我应该愿意以价格p购买“是”代币，使得p<x（假设我不介意风险）。同样，我应该愿意以价格p<100-x购买“否”代币。此外，我也愿意出售这些代币，只是改变不等式符号。这创造了一个市场，人们可以相互交流并做出对他们信仰的承诺。一旦结果已经确定，就会开放转换，参与者可以转换他们的代币。假设费城老鹰队确实获胜，那么以任何低于100 NAM的价格购买“是”代币的人将能够获利。

虽然公开在透明的区块链上进行此操作有好处，正如Vitalik Buterin所解释的那样，但进行私有操作也有好处。也许你不想让你的费城出生的朋友（例如Brent Stone）知道你在超级碗上押了反对他们的球队获胜的赌注。

转换电路： 在不确定结果之前 在结果变得确定之后 如果SuperBowl.winner == 'Eagles': 否则:

NFT升级 在隐私集合中也可以实现可编程非同质代币。一个示例是PokéNAM，它希望在私下演化。幸运的是，如果存在正确的转换电路，这是完全可能的。例如：

[−1] CharNAMder [−81000] EXP [+1][CharNAMeon]

在这里，唯一的限制是想象力。

隐私借贷协议

这个想法需要一些想象力，不仅仅是一个转换电路，还需要额外的逻辑才能实现。最直接的例子是允许匿名出借和伪匿名借款。这是可能的，因为通证化的借贷是直接可替代的，但由于抵押品要求，通证化的借款则不是。

以借出ETH为例。实现这一点的一个可能的方法（也许是幼稚的）是创建以下转换：

其中i epoch是每期的利率。ΔEPOCH是时期之间的差异。然后，一个VP（验证谓词）将处理（使用透明地址）允许借款用户以抵押品的方式借NAM。通过这种方式，如果借款人达到了清算阈值（理想情况下是100%以上的抵押品），清算可以通过套利来去中心化进行。换句话说，人们可以使用我们今天在像AAVE这样的应用中所拥有的标准去中心化借贷设置。

为了实现隐私借贷，需要进一步的想象力。现在，我们需要一种方法，将抵押品进行池化，而不会将太多的风险转移到借款人或借款人之间。实施需要非常小心，以防信息不对称引发不好的影响。

前两个额外的转换率比较容易理解：

💡 电路部分I

然而，我们现在需要解决另外两个更难的问题。借款人有什么激励来支付他们的利息？是什么激励借款人确保他们的抵押阈值得到满足？如何协调借入的NAM和NAM之间的差异，因为这些资产不再可替代。

一个提出的解决方案是通过定期支付“抵押债务”的方式激励“重新转换”NAM。这将添加几个新的转换率：

💡 电路部分II

[+r j] ETH [−i epoch∗(ΔEPOCH)] NAM

如果您提供了足够的额外抵押品和利息，那么您可以将旧时期的借入NAM从某个旧时期转换为当前时期的指定NAM。这种实施方法可能会非常复杂，需要每个时期添加一个新的转换，以最小化风险。这样，流通中的借款资产应始终具备足够的抵押品。这只是作为借出者寻求退出的最后手段应该使用的一个转换。然后，借入的NAM可以转换回其抵押品，因为所有债务都将通过转换1进行偿还。处理清算绝对是使这项工作变得最困难的部分，因为你希望将抵押品的放置保持匿名。

具有非动态转换电路，这将必须使用固定的利率来完成。但是，使用动态可编程的转换电路（请参阅https://github.com/anoma/taiga👀），应该可以以更经济高效的方式处理供需。

结论

简而言之，MASP技术背后的内容远不止其名称所示的那样。与转换电路结合使用，该技术变得特别强大，允许各种潜在应用。在Namada，我们专注于提供安全的隐私支付系统（目前），但我们希望一些读者能够吸收转换电路背后的思想，并将其用于实现和发明可以真正推动ZK应用前沿的新颖创意。

脚注

[1]：有关更多详细信息，请参阅Sasson，Eli Ben等人的论文“Zerocash: Decentralized anonymous payments from bitcoin”，2014 IEEE安全与隐私研讨会，IEEE，2014。

[2]：资产类型比人们可能期望的更加普遍。Namada上的资产类型也可以用来表示时期资产（例如$NAM_时期_42$）。时期资产在转换电路中发挥作用。

[3]：有关转换电路的更多信息，请参阅相关部分。